F(x) = ντο – ρε – μι
[dropcap size=big]Έ[/dropcap]λα. Πες την αλήθεια. Από το 1 έως το 10, πόσο σιχαίνεσαι τα μαθηματικά; Αμέτρητες ώρες υπερκατανάλωσης φαιάς ουσίας μόνο και μόνο για να δεις κι άλλους αριθμούς να ξεχύνονται σε ιδρωμένα σπιράλ τετράδια! Κι όμως, η συγκεκριμένη επιστήμη έλαβε άφεση αμαρτιών, περίπου 2,5 χιλιάδες χρόνια πριν, την ημέρα που άρχισε να χτίζει την 3η τέχνη… τη μουσική!
Οι Πυθαγόρειοι, ήδη, χώριζαν τα μαθηματικά σε τέσσερις κατηγορίες: την αριθμητική, τη γεωμετρία, την αστρονομία και τη μουσική. Σύμφωνα, λοιπόν, με σχετικές θεωρίες, η τάξη της μουσικής είναι μαθηματική τάξη και τη διέπουν μαθηματικές αρχές. Ως εξέλιξη της θεωρίας αυτής, αποδείχθηκε ότι οι σχέσεις μεταξύ των νοτών εκφράζονται με απλή μαθηματική φόρμουλα. Φανταστείτε, λοιπόν, σε κάθε πεντάγραμμο που θα τύχει να πιάσετε στα χέρια σας, τις νότες μπροστά σας να μετατρέπονται σε αριθμητικά στοιχεία.
[dropcap size=big]Κ[/dropcap]άνοντας άθελά του την αρχή, ο Πυθαγόρας ανακάλυψε τυχαία τη σχέση μεταξύ μαθηματικών και μουσικής περνώντας έξω από ένα… σιδηρουργείο. Την προσοχή του απέσπασε η διαδοχή από διαστηματικές σχέσεις που προέρχονταν από χτυπήματα σφυριών στο αμόνι. Παρατήρησε πως η διαφορά ήχου δε σχετιζόταν με τη δύναμη του χτύπου, αλλά με το βάρος των σφυριών. Πειραματίστηκε αρκετά για να αποδείξει και να εξελίξει την παραπάνω παρατήρηση. Συνέχισε με τη θεωρία των σφαιρών, η οποία περιγράφεται ως το σύνολο ήχων που δεν ακούγονται, αλλά παράγονται από την περιστροφή των πλανητών, ανάλογα με την απόστασή τους από τη γη. Τέλος, απέδειξε μαθηματικά τη μουσική ασυμμετρία και τη συσχέτιση μεταξύ μαθηματικής και μουσικής ανθυφαίρεσης.
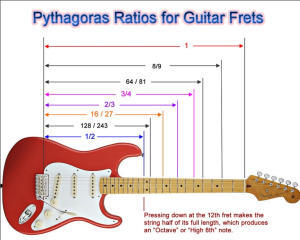
Πρωταγωνιστικό ρόλο στον αρχικό έμπρακτο πειραματισμό του ήχου και του μέτρου έπαιξε αναμφίβολα το μονόχορδο. Ένα μουσικό έγχορδο με μία ή δύο χορδές και έναν κινητό καβαλάρη που πίεζε τη δεσμευμένη χορδή με αποτέλεσμα να «διαιρεί» το μήκος της. Με τον τρόπο αυτό επιτρεπόταν η αλλοίωση του ύψους του τόνου μέσω μαθηματικής φόρμουλας. Έτσι, διαπιστώνουμε τα παρακάτω έκδοχα: ‘Οταν μοιράσουμε τη χορδή ΑΚΡΙΒΩΣ στο μέσον της θα πάρουμε τον λόγο 1/2 και τον τόνο μία οκτάβα ακριβώς υψηλότερο. Αντίστοιχα, τα 3/4 παράγουν μία τέταρτη και τα 2/3 μία πέμπτη. Τα 4/5 της χορδής θα μας δώσουν μία μεγάλη τρίτη, ενώ τα 5/6 μία τρίτη μικρή!
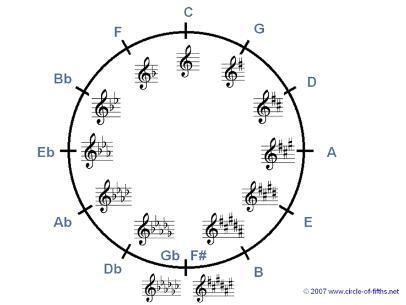[dropcap size=big]Κ[/dropcap]ι όμως, οι αρχαίοι Έλληνες, οι επιστήμονες (και ψυχάκιδες), δεν είναι οι μόνοι που ασχολούνται με το συγκεκριμένο πάντρεμα επιστήμης και τέχνης. Ολόκληρα ρεύματα μουσικής, όπως η Mathrock και η Mathcore, έχουν βασίσει τον ήχο τους σε μαθηματικές ιδιαιτερότητες. Το ύφος τους χαρακτηρίζεται από περίτεχνα ρυθμικούς συνδυασμούς, άτυπες ρυθμικές δομές (ανώμαλα και ξαφνικά σταματήματα-ξεκινήματα), αντίστιξη, περίεργες χρονικές αξίες και μέτρα, αλλά και παρατεταμένες, έως συχνά παράφωνες, συγχορδίες. Ένα άκουσμα διαφορετικό, και ίσως ακατανόητο, διόλου εφάμιλλο του μέσου ακούσματος, μα τόσο διαπεραστικά και θετικά περίεργο που δε δίνει περιθώριο να περάσει απαρατήρητο.
Απρόσμενα, αριθμοί και νότες δεν αποτελούν έννοιες αρκετά αποξενωμένες η μία από την άλλη. Αλλά πώς να φανταστεί κανείς πως κάτι τόσο καταδικασμένα μονόχνοτο μπορεί να δημιουργήσει την αφορμή για τις πιο ζωντανές στιγμές και αναμνήσεις! Ξανασκέψου το… Ίσως τελικά δεν μισείς τα μαθηματικά όσο νομίζεις!
Κείμενο: Λυδία Νικολαΐδη (Lavart)
